Quantum computer reveals atomic dynamics of photosensitive molecules

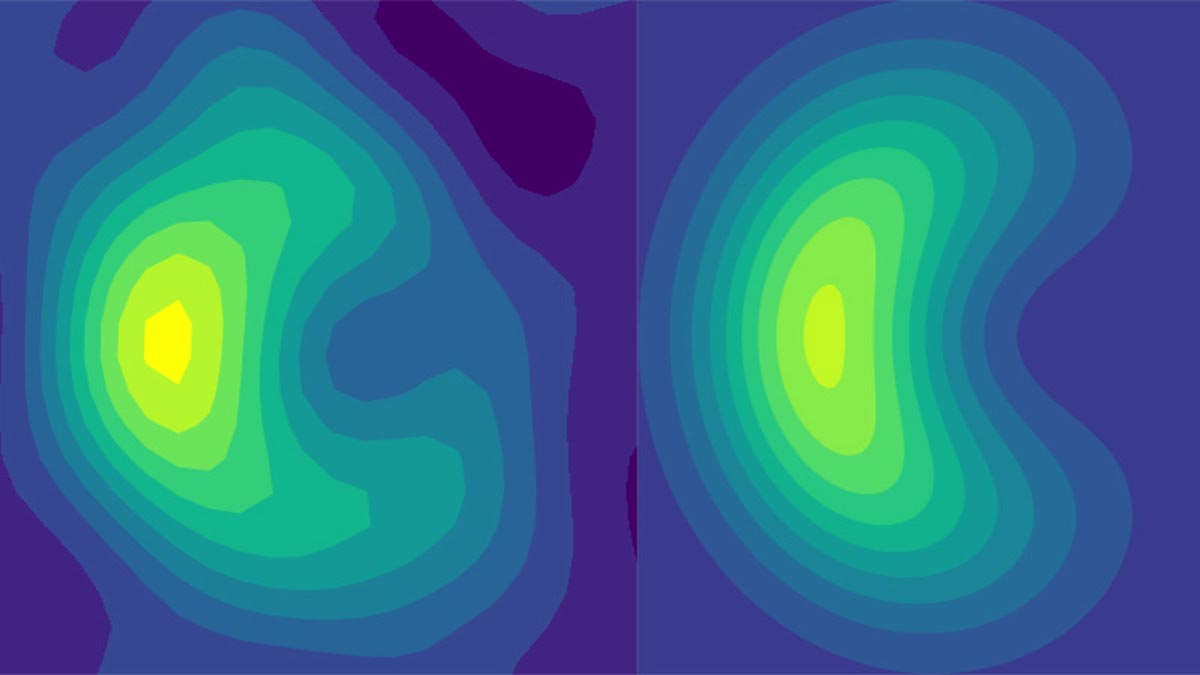
Experimental results from a quantum computer (left) that align well with theory (right) are the first quantum-based method to demonstrate a quantum effect in the way light-absorbing particles interact with incoming photons. Credit: Jacob Whitlow, Duke University

A quantum computer has slowed simulated molecular quantum effects by a billion times, allowing researchers to measure them directly for the first time.

Researchers at Duke University have applied a quantum-based method to observe the quantum effect in the way light-absorbing molecules interact with incoming photons. This effect, known as conic crossing, places limits on the paths molecules can take to change between different configurations.

The observation method uses a quantum simulator, which was developed through research in Quantitative statisticsaddresses a long-standing fundamental question in chemistry that is critical to processes such as PhotosynthesisVision and photostimulation. It is also an example of how advances in quantum computing can be used to study basic science.

The results are published August 28 in the journal Nature Nature chemistry.

Conic intersections

Kenneth Brown, Michael J. . “This limitation, called the geometric phase, is not impossible to measure, but no one has been able to do it. Using a quantum simulator has given us a way to see it in its natural quantum existence.

Conical intersections can be imagined in the form of a mountain top touching the tip of its reflection coming from the top and controlling the movement of electrons between energy states. The lower half of the conic cross represents the energy states and physical locations of the unexcited molecule in its ground state. The top half represents the same molecule but with its excited electrons, having absorbed energy from an incoming photoparticle.

The molecule cannot remain in the higher state, as its electrons are out of position with respect to their host atoms. To return to a more favorable lower energy state, the atoms of the molecule begin to rearrange themselves to meet electrons. The meeting point of the two mountains – the conical intersection – marks the inflection point. The atoms can either fail to make it to the other side by readjusting to their original state, dumping excess energy into the surrounding molecules in the process, or they can successfully make the switch.

Quantum effects in molecules

Because atoms and electrons move so quickly, they exhibit quantum effects. Rather than being in any one shape – in any one place on the mountain – at any given time, the molecule actually takes many forms at once. One could think of all of these potential sites as represented by a blanket wrapped around a section of mountainous landscape.

However, due to a mathematical flaw in the system that emerges from the underlying mathematics, called the geometric phase, certain molecular transformations cannot occur. The blanket cannot completely wrap around the mountain.

“If a molecule has two different paths to get to the same final shape, and those paths surround a conical intersection, then the molecule can’t take that shape,” said Jacob Whitlow, a PhD student working on the molecule’s development. In the Brown laboratory. “It’s a hard-to-understand effect, because the geometric phase is strange even from a quantum-mechanical point of view.”

Engineering phase measurement challenges

Measuring this quantum effect has always been difficult, because it is short-lived, on the order of femtoseconds, and small, on the scale of atoms. Any disruption of the system will prevent its measurement. While many small pieces of the larger conic cross phenomenon have been studied and measured, the engineering phase has always eluded researchers.

Quantum computers in research

“If conic intersections exist — which they do — then the geometric phase must be present,” said Brown, who also holds appointments in physics and chemistry at Duke University. “But what does it mean to say there is something you cannot measure?”

In this paper, Whitlow and colleagues use a five-ion quantum computer built by the group of Joongsang Kim, Distinguished Professor of Electrical and Computer Engineering at Cicciano University. A quantum computer uses lasers to manipulate charged atoms in a vacuum, providing a high level of control. Whitlow and Guping Jia, a doctoral student in Brown’s lab, also expanded the system’s capability by developing ways to actually nudge floating ions inside their electromagnetic traps.

Depending on how the ions move and the quantum state they’re placed in, they can exhibit essentially the same quantum mechanics as the movement of atoms around a conical crosshair. Because the quantum dynamics of the trapped ions are about a billion times slower than the dynamics of the molecule, the researchers were able to make direct measurements of the geometry in action.

The results look like a two-dimensional crescent. As shown in the conic intercept diagram, some formations on one side of the cone fail to reach the other side of the cone even though there is no energy barrier. Brown says the experiment is a great example of how today’s rudimentary quantum computers can model and reveal the inner quantum workings of complex quantum systems.

“The beauty of the trapped ions is that they get rid of the complex environment and make the system clean enough to make these measurements,” Brown said.

Independent experience in Sydney University, Australia also observed geometric phase effects using a quantum ion-trap simulator. The approach varies in many technical details, but the overall observations are consistent. Sydney’s work will be published in the same issue of Nature chemistry.

Reference: “Simulation of Conic Intersections with Trapped Ions” By Jacob Whitlow, Zhubing Jia, Yi Wang, Zhao Fang, Gongsang Kim, and Kenneth R Brown, 28 Aug. 2023, Available here. Nature chemistry.
doi: 10.1038/s41557-023-01303-0

This work was supported by the Intelligence Advanced Research Projects Activity (W911NF-16-1-0082), the National Science Foundation (Phy-1818914, OMA-2120757), and the DOE Office of the QSCOUT Program for Advanced Scientific Computing Research (DE-0019449). ), Army Research Office (W911NF-18-1-0218).